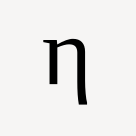I know that we can brute force it by placing an obstacle at every valid position in the path, but is there a more elegant / efficient solution?
One optimization some used was to detect loops by only recording the turning points instead of all walked tiles.
I haven’t attempted this approach, but this has been on my mind a lot. I think if you keep track of all turning positions in the first run, you can run through pairs of turning positions and imagine a line extending until it hits an obstacle. I think you’d need to iterate in order of turns, and extend backwards the earlier turn in a pair, and extend forwards the later turn in the pair.
If the extended paths for two turns intercept, that is a point that an added obstacle would make a loop. I’m not 100% sure mathematically this is true, but there’s less turns than there are steps, so performing the tests on turns should be faster.
Using the option 4 in the example, this is what the extended lines would look like as
vfor the backwards line and<as the forward line from the turn as noted by the+. Thexis where these lines meet. If they don’t intercept, then adding an obstacle wouldn’t result in a loop forming:....#..... .........# .......... ..#....... ..+....#.. ..v....... .#v....... ..v.....#. #<x<<<+... ..v...#...I’ll try to attempt this if I have time and see how it performs, but hoping someone else can check me on this and see if this is not practical.
EDIT: I attempted this and it works with the sample, but only finds about 25% of the obstacles for the real input. It’s pretty tedious to debug the big map unfortunately, so I’m not sure which obstacles are being missed. I do think this is the right approach though and is so fast and elegant, if only it worked…
EDIT 2: Updated graph with better information
That’s a neat idea, but isn’t it possible that adding an obstacle could send the guard into a loop in a previously unexplored part of the map? I think you’d miss that case.
I’m not sure I understand the concern, maybe a visualization would help describe what you’re talking about? I updated my comment to describe my process in better detail, it was confusing before. I’m only focused in checking unobstructed straight lines from places where the guard has turned, so I don’t think it could get into unexplored areas.
I’m imagining something like this:
.#........ ....#..#.. .O.......# .........# ......#... .^......#.The original path hits the leftmost two obstructions, whereas the new path avoids these but hits all the others (and loops).
Ois not on an intersection of any two turns in the original path. It is if you check all possible turning points, although there’s potentially a lot more of them.Ohh that is helpful, yeah, i don’t know how I’d get these counted. This is probably the ones I’m missing. The way I’ve been thinking about it is that all a loop is is a rectangle. So basically each guard’s turn is a corner of a rectangle. By taking opposite corners (every other turn the guard makes) we can see if we can draw a full rectangle without hitting any walls. If we can, then that would make a loop.
A few things I figured out playing with this:
- You need to pay attention to the rotation rule of the guard. Taking any random rotation points won’t take the guards rotation into effect and will result in false positives.
- Thinking about the rectangle visualization, since you’re only trying to test opposite corners, you only need to compare one turn and turn + 2 to see if they finish the rectangle.
So maybe the logic would be to ignore the rotations in part one when the guard walks unobstructed, and do a pass through the whole map and mark each point of a possible rotation, and then drawing possible rectangles where 3 corners exist, to find an obstruction point. Then you can check if the obstruction point is in the set of steps the guard made in part 1 when unobstructed. Still though, I think this doesn’t take into account the guards rotation, so will probably be wrong.
Rectangles don’t account for all loops though, right? Couldn’t you have a loop with, say, 6 points in an L shape?
Yeah you’re right. I keep focusing on the smaller example where everything is just rectangle loops, but the big map is way more complex. I do wonder though if an L shaped loop is just multiple rectangle loops combined though? Like if you can find all the rectangles, then find ones where combined they make bigger loops?
I mean, sure you can combine rectangles to make any path, but since there is no upper limit I don’t think that will help much. You may be on to something and I just can’t see it, though! Good luck!
You gave me an idea!
- Give each obstacle in the initial map an ID, and build three indexes by ID, by row, and by column.
- Use the list of obstacles to build up a map from
(ID, direction)to(next ID, direction)(if any) – that is, for each obstacle, update the map entry for any preceding obstacle that could reach it. - This map can be used to compute the path very cheaply.
- And crucially, you can easily update the map for new obstacles using the same method above.
I think this would give a pretty good speed up, and you might not need to worry about only checking intersections.
I’m also struggling with part 2. At the moment I am following the path and in each place I look if can connect with an earlier part of the path to the right by placing an obstacle, but without cutting off another earlier part of the path with that obstacle. I have indexes for each path location to see where in the path they first appear.
However at the moment I still have a bug counting too many possibilities. Any other ideas?
I am using same solution, and getting right count with test input, but the actual input gives too many.
Annoying, and really hard to debug. I made renderer to visualize, but unable to find the bug.
One misunderstanding was that I counted same walls twice, because the result should not count same added wall twice if it has same x,y.
Yeah something like that happend for me too, and later I counted too little because it would not recognise some possible solutions. Finally I solved it by just walking along the path and at each location put an obstacle in front of it and then check if the changed map results in a path enters longer than 10000 steps. Not pretty but at least it lead to the right result with a runtime of ~3 seconds. I would have saved a lot of time if I had tried the “brute force” way before, so I guess lesson learned.
You can track by just keeping list of all positions and movement direction, if two are same, it means that it is in a loop.